Information Theory Lab: Research
My research interests are primarily centered around information theory and its applications to various areas, listed below. Our recent tutorials on "Deep learning and information theory" at ISIT 2018 , "Algorithms for high-throughput sequencing" at BCB 2016 and "High Throughput Sequencing: The Microscope in the Big Data Era" at ISIT 2014 convey a birds-eye view of some aspects of our research.
- Blockchain Systems
- Deep Learning and information theory
- Information measures and estimators
- Computational Biology
- Wireless Networks
Blockchain Systems
Optimal latency and throughput in blockchains
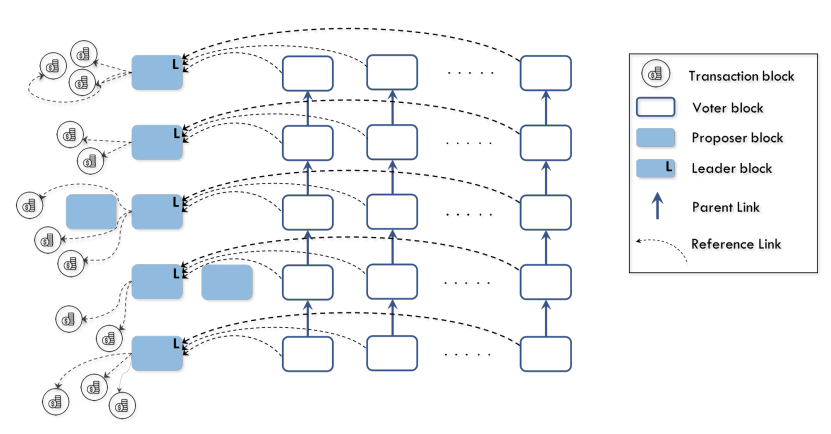 |
The concept of a blockchain was invented by Satoshi Nakamoto to maintain a distributed ledger for an electronic payment system, Bitcoin. In addition to its security, important performance measures of a blockchain protocol are its transaction throughput, confirmation latency and confirmation reliability. These measures are limited by two underlying physical network attributes: communication capacity and speed-of-light propagation delay. Existing systems operate far away from these physical limits. In this work we introduce Prism, a new blockchain protocol, which can provably achieve 1) security against up to 50% adversarial hashing power; 2) optimal throughput up to the capacity C of the network; 3) confirmation latency for honest transactions proportional to the propagation delay D, with confirmation error probability exponentially small in the bandwidth-delay product CD; 4) eventual total ordering of all transactions. Our approach to the design of this protocol is based on deconstructing the blockchain into its basic functionalities and systematically scaling up these functionalities to approach their physical limits. V. Bagaria, S. Kannan, D. Tse, G. Fanti, and P. Viswanath, "Deconstructing the Blockchain to Approach Physical Limits," to appear in ACM ACM Conference on Computer and Communications Security (CCS 2019). Preprint: arxiv. Videos: (1) Talk at Stanford (2) Animation of algorithm |
Coding theory for blockchains
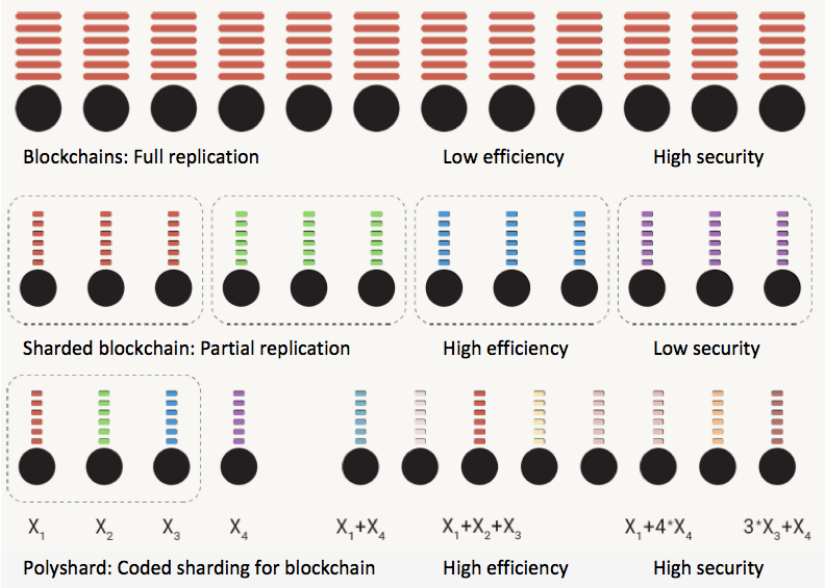 |
Today's blockchains do not scale in a meaningful sense. As more nodes join the system, the efficiency of the system (computation, communication, and storage) degrades, or at best stays constant. A leading idea for enabling blockchains to scale efficiency is the notion of sharding: different subsets of nodes handle different portions of the blockchain, thereby reducing the load for each individual node. However, existing sharding proposals achieve efficiency scaling by compromising on trust - corrupting the nodes in a given shard will lead to the permanent loss of the corresponding portion of data. We observe that sharding is similar to replication coding, which is known to be inefficient and fragile in the coding theory community. In this paper, we demonstrate a new protocol for coded storage and computation in blockchains. In particular, we propose PolyShard: "polynomially coded sharding" scheme that achieves information-theoretic upper bounds on the efficiency of the storage, system throughput, as well as on trust, thus enabling a truly scalable system. We provide simulation results that numerically demonstrate the performance improvement over state of the arts, and the scalability of the PolyShard system. Finally, we discuss potential enhancements, and highlight practical considerations in building such a system.
S. Li, M. Yu, S. Avestimehr, S. Kannan, and P. Viswanath
|
Deep learning and information theory
Communication algorithms via deep learning
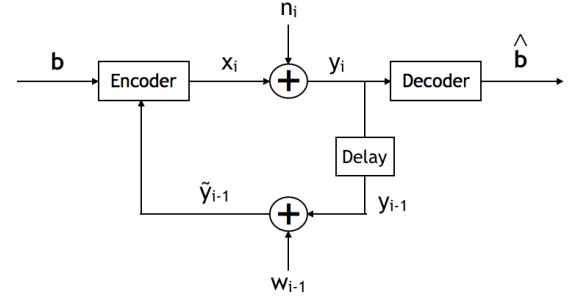 |
The design of codes for communicating reliably over a statistically well defined channel is an important endeavor involving deep mathematical research and wide-ranging practical applications. In this work, we present the first family of codes obtained via deep learning, which significantly beats state-of-the-art codes designed over several decades of research. The communication channel under consideration is the Gaussian noise channel with feedback, whose study was initiated by Shannon; feedback is known theoretically to improve reliability of communication, but no practical codes that do so have ever been successfully constructed. We break this logjam by integrating information theoretic insights harmoniously with recurrent-neural-network based encoders and decoders to create novel codes that outperform known codes by 3 orders of magnitude in reliability. We also demonstrate several desirable properties of the codes: (a) generalization to larger block lengths, (b) composability with known codes, (c) adaptation to practical constraints. This result also has broader ramifications for coding theory: even when the channel has a clear mathematical model, deep learning methodologies, when combined with channel-specific information-theoretic insights, can potentially beat state-of-the-art codes constructed over decades of mathematical research. We also show how to construct decoders for known channels. H. Kim, Y. Jiang, S. Kannan, S. Oh, and P. Viswanath, "Feedback Codes via Deep Learning," NIPS 2018, Arxiv H. Kim, Y. Jiang, S. Kannan, S. Oh and P. Viswanath, "Communication Algorithms via Deep Learning," ICLR 2018, Arxiv. |
Information theoretic limits for parameter inference in neural networks
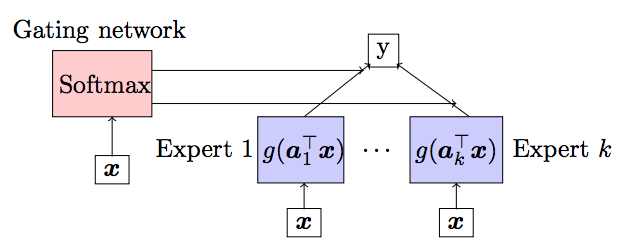 |
In recent years, gated recurrent neural networks (RNNs) such as LSTM (Long-Short-Term-Memory) and GRU (Gated-Recurrent- Unit) have shown remarkable successes in a variety of challenging machine learning tasks. A key interesting aspect and an important reason behind the success of these architectures is the presence of a gating mechanism that dynamically controls the flow of the past information to the current state at each time instant, unlike a vanilla RNN. Surprisingly, despite their widespread popularity, there is very little theoretical understanding of these models. For example, basic questions such as the learnability of their parameters still remain open. In this project, we view gated recurrent neural networks with an information theoretic lens. We recently made an interesting and non-trivial connection that gated RNNs are composed of a building block, known as Mixture-of-Experts (MoE). In fact, much alike LSTMs/GRUs, MoE is itself a widely popular gated neural network architecture and has been the subject of great research. However, provable parameter inference is a long-standing open problem in such networks - we solve this problem by using tensor methods. A. Varadhan, S. Kannan, S. Oh and P. Viswanath. Globally Consistent Algorithms for Mixture of Experts. |
Information measures and estimators
Potential Influence Measures
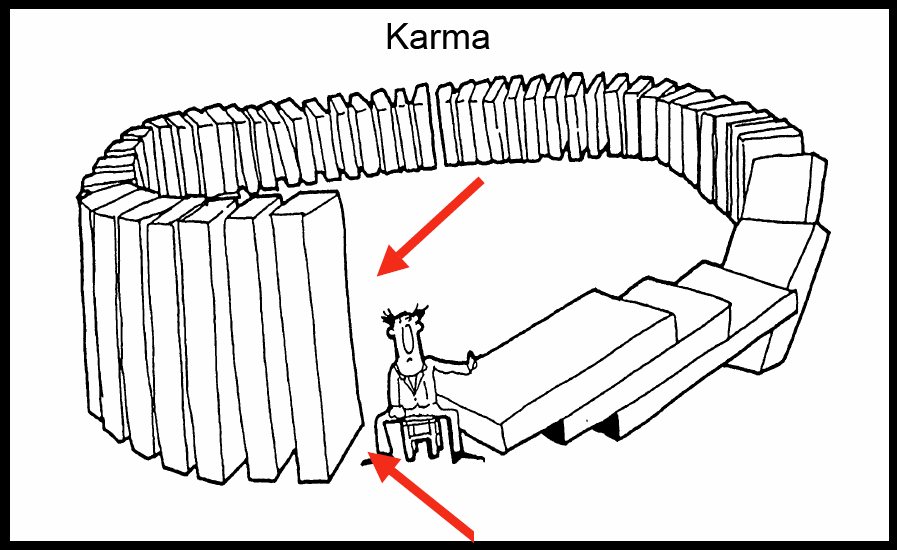 |
There has been a long history of studying measures of relationship between a pair of random variables. These measures are typically symmetric and furthermore, depend on the joint distribution of the two variables. We propound a new class of influence measures for studying strength of causality, which are asymmetric, and depend only on the conditional distribution of the effect given the cause. We term such measures as potential measures, as they account for the potential influence of the effect given the cause, instead of the factual influence of the effect given the cause. We conduct an axiomatic study of dependence measures on conditional distributions. Shannon capacity, appropriately regularized, emerges as a natural measure under these axioms. We examine the problem of calculating Shannon capacity from the observed samples and propose a novel fixed-k nearest neighbor estimator, and demonstrate its consistency. Furthermore, we extend this concept to conditional mutual information, and develop appropriate estimators, motivated by applications in time-series problems, particularly arising from gene network estimation. A. Rahimzamani and S. Kannan, "Potential Conditional Mutual Information," Allerton 2017, Arxiv. W. Gao, S. Kannan, S. Oh, and P. Viswanath, "Conditional dependence via shannon capacity: Axioms, estimators and applications," in Proceedings of The 33rd International Conference on Machine Learning (ICML), 2016, Arxiv |
Estimators for discrete-continuous mixtures
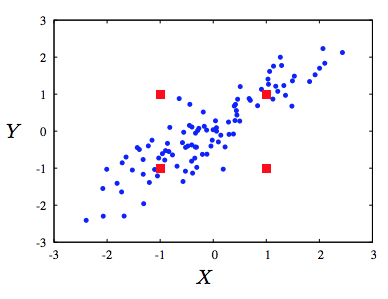 |
Information theoretic quantities play an important role in various settings in machine learning, including causality testing, structure inference in graphical models, time-series problems, feature selection as well as in providing privacy guarantees. A key quantity of interest is the mutual information and generalizations thereof, including conditional mutual information, multivariate mutual information, total correlation and directed information. While the aforementioned information quantities are well defined in arbitrary probability spaces, existing estimators add or subtract entropies (we term them ΣH methods). These methods work only in purely discrete space or purely continuous case since entropy (or differential entropy) is well defined only in that regime. We invent new estimators for mutual information that work in the general case. Furthermore, we define a general graph divergence measure (𝔾𝔻𝕄), as a measure of incompatibility between the observed distribution and a given graphical model structure. This generalizes the aforementioned information measures and we construct a novel estimator via a coupling trick that directly estimates these multivariate information measures using the Radon-Nikodym derivative. These estimators are proven to be consistent in a general setting which includes several cases where the existing estimators fail, thus providing the only known estimators for the following settings: (1) the data has some discrete and some continuous-valued components (2) some (or all) of the components themselves are discrete-continuous mixtures (3) the data is real-valued but does not have a joint density on the entire space, rather is supported on a low-dimensional manifold. We show that our proposed estimators significantly outperform known estimators on synthetic and real datasets. W. Gao, S. Kannan, S. Oh, and P. Viswanath, "Estimating Mutual Information for Discrete-Continuous Mixtures," in Proceedings of The Neural Information Processing Conference (NIPS), Dec. 2017, Spotlight paper, Arxiv. A. Rahimzamani, H. Asnani, P. Viswanath and S. Kannan, "Estimators for Multivariate Information Measures in General Probability Spaces," Proc. Neural Information Processing Systems (NIPS), Dec. 2018, Arxiv. |
Deep Learning for Property Testing
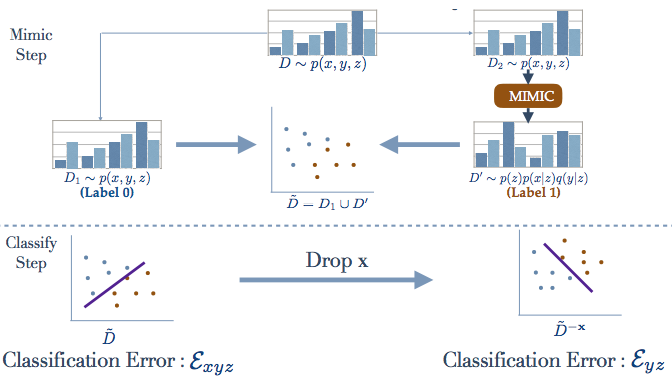 |
Given independent samples generated from the joint distribution p(x, y, z), we study the problem of Conditional Independence (CI-Testing), i.e., whether the joint equals the CI distribution p CI (x, y, z) = p(z)p(y|z)p(x|z) or not. We cast this problem under the purview of the proposed, provable meta-algorithm, "Mimic and Classify", which is realized in two-steps: (a) Mimic the CI distribution close enough to recover the support, and (b) Classify to distinguish the joint and the CI distribution. Thus, as long as we have a good generative model and a good classifier, we potentially have a sound CI Tester. When the data is high-dimensional, the classical statistical methods have poor performance. A key requirement in practice is to have provable p-value control, as well as good performance. In this work, we show how to couple deep learning with classical statistical methods to obtain p-value control as well as good empirical performance. We leverage both generative and classification methods from the modern advances in Deep Learning, which in general can handle issues related to curse of dimensionality and operation in small sample regime. Since classification methods are better developed than generative models, we show how to do bias-cancellation to handle mis-estimation at the generative model. R Sen, K Shanmugam, H Asnani, A Rahimzamani, S Kannan, "Mimic and Classify: A meta-algorithm for Conditional Independence Testing," Arxiv. |
Computational Biology
Causal Learning and Gene Network Inference
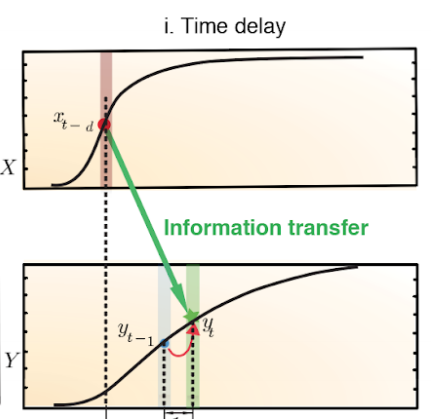 |
While understanding correlation between variables gives predictive power, understanding causal connections between variables gives power to intervene and perturb the system. In order to do this, the time series of each variable, i.e., the corresponding random process, can provide valuable information. In this project, we explore the reverse engineering of causality networks using observed time series of variables. this problem is well studied if the time-series are real valued, for example, Granger causality provides a good metric, there is very little work for the case of discrete variables. We propose a new method that can reverse engineer the causal network between boolean random processes under a certain model assumption, inspired from neuroscience. We are currently exploring the fundamentals of causal learning and its applications in computational biology. In particular, we develop a toolkit Scribe, which can infer gene regulatory information using restricted directed information. Furthermore, we advocate the use of coupled time-series measurement technologies to get better signal for gene-network inference. X. Qiu, A. Rahimzamani, L. Wang, Q. Mao, T. Durham, J. McFaline-Figueroa, L. Saunders, C. Trapnell, and S. Kannan "Towards inferring causal gene regulatory networks from single cell expression measurements," biorxiv . H. Hosseini, S. Kannan, B. Zhang, and R. Poovendran, "Learning temporal dependence from time-series data with latent variables," IEEE DSAA 2016. A. Rahimzamani and S. Kannan "Network inference via directed information: The deterministic limit," Allerton 2015. S. Kannan and T. Zheng, A Method for Inferring Causal Dependencies between Random processes, U.S. Patent |
Single Cell RNA-Seq Data Analytics
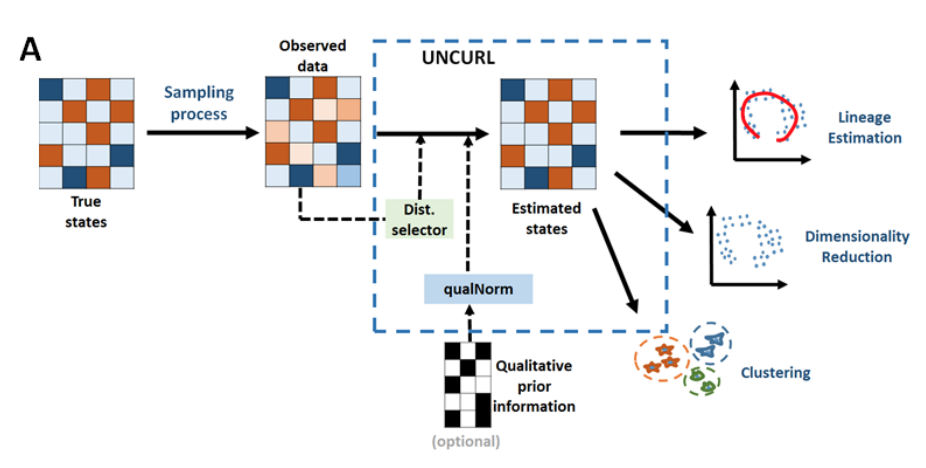 |
Single cell RNA-seq (scRNA-seq) data contains a wealth of information which has to be inferred computationally from the observed sequencing reads. As the ability to sequence more cells improves rapidly, existing computational tools suffer from three problems. (1) The decreased reads per-cell implies a highly sparse sample of the true cellular transcriptome. (2) Many tools simply cannot handle the size of the resulting datasets. (3) Prior biological knowledge such as bulk RNA-seq information of certain cell types or qualitative marker information is not taken into account. Here we present UNCURL, a preprocessing framework based on non-negative matrix factorization for scRNA-seq data, that is able to handle varying sampling distributions, scales to very large cell numbers and can incorporate prior knowledge. S. Mukherjee, Y. Zhang, S. Kannan, and G. Seelig, "Scalable preprocessing for sparse scRNA-seq data exploiting prior knowledge," Bioinformatics |
Fundamental Limits and Optimal Algorithms for Transcriptome Assembly
 |
High throughput sequencing of RNA transcripts (called RNA-seq) has emerged in recent years as a powerful method that enables discovery of novel transcripts and alternatively spliced isoforms of genes, along with accurate estimates of gene expression. A key step in RNA-seq is assembly of transcripts from short reads obtained using shotgun sequencing. While there are some existing assemblers, they do not always agree on the reconstructed transcripts even when the number of reads is large. Therefore we raise the following fundamental question: when is there enough information to do accurate transcriptome reconstruction? We establish the information theoretic limits on this assembly problem in the limit of large number of reads. We also propose a new algorithm for transcriptome recovery that has near optimal performance, and yet has low complexity. One aspect of the proposed algorithm is derived from a new method we propose for decomposing a flow into the fewest number of paths. In this ongoing project, we are in the process of building a software system capable of high performance transcriptome assembly. Some open theoretical questions we are investigating include the role of a reference genome, a reference transcriptome, and the utility of long reads. S. Kannan, J. Hui, K. Mazooji, L. Pachter and D. Tse, Shannon: An Information-Optimal de Novo RNA-Seq Assembler preprint on biorxiv. |
Fundamental Limits and Optimal Algorithms for DNA Variant Calling
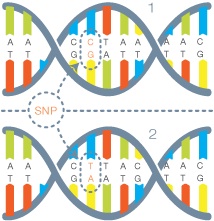 |
DNA variant calling is a basic problem in computational biology:one would like to know how different is a target DNA (for example, a particular individuals DNA) from a known reference DNA (for example, a reference human genome). The standard approach is to perform shotgun sequencing on the target DNA, i.e., to obtain a set of short reads obtained as substrings from the target DNA sequence. The goal of the reconstruction algorithm is to characterize the variations in the target DNA from the reference DNA using the short reads. While there are different algorithms for calling different types of variation, for example, substitution, insertion/deletion (indel), structural variant, there is no theory nor a guiding principle behind when these algorithms are optimal. In this project, we seek to establish the fundamental limits of variant calling and propose new algorithms that can approach these limits. We also quantify the benefits of having the side information in the form of a reference DNA. In this ongoing project, we are in the process of building a reference based genome assembler. S. Kannan, S. Mohajer and D. Tse, Fundamental Limits of DNA Variant Calling, Allerton 2014. |
Wireless Networks
Capacity of Wireless Interference Networks
 |
The density of wireless deployment is steadily increasing and interference between wireless devices will place a key bottleneck on communication networks. The current solution of orthogonal resource allocation will not scale well in this limit. In this project, we study the capacity of a network of nodes sharing a wireless medium, with several soures intending to communicate to several destinations. We show a general meta-theorem, which we prove for a variety of settings: If there is a "good" scheme for a channel, which is approximately cut-set acheiving and reciprocal, then for a network of such channels, local coding plus global routing is optimal to within a logarithmic factor in the number of messages. This information theoretic result establishes also that a simple layered architecture for communication is optimal, if it is carefully designed with the correct boundaries for the layers. Key technical contributions include a formal connection of the network information theory problem to the theory of approximation algorithms and the ruling out of more complex schemes in order to achieve the capacity to within the approximation factor. S. Kannan and P. Viswanath, Capacity of multiple unicasts in wireless networks: A polymatroidal approach, IEEE Trans. Info. Theory, final revision. S. Kamath, S. Kannan, and P. Viswanath, Wireless Networks with Symmetric Demands , IEEE ISIT, journal version in submission. |
Approximation Algorithms for Polymatroidal Networks
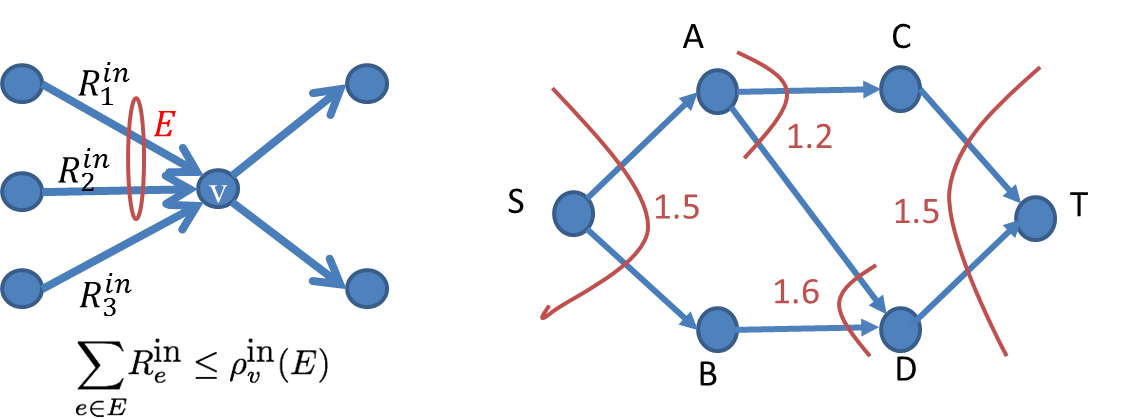 |
Networks are normally modelled to have edge or node capacities that constrain communication rate on a given edge or a node. However, several real world networks, including wireless and transportation networks, may display more complicated coupling of capacity constraints between edges and nodes. In this project, we "rediscover" a polymatroidal network model, where the capacity of edges that meet at a node, are jointly constrained by a submodular function. We show that for this model, the classical flow-cut gap results for the multicommodity problem can be generalized to this model. This model captures existing results on node and edge capacitated networks, and also single-commodity results for polymatroidal networks, which are originally derived using differing methods inside a single conceptual umbrella. The key technical contribution is the use of convex relaxation of the combinatorial cut problem using the Lovasz extension and a rounding scheme for the relaxed cut problem using line embeddings. Furthermore, we demonstrate applications of this result in deducing the capacity of wireless networks. C. Chekuri, S. Kannan, A. Raja, and P. Viswanath, Multicommodity flows and cuts in polymatroidal networks, SIAM Journal on Computing, under review. |
Capacity of Broadcast Networks with Relaying and Cooperation
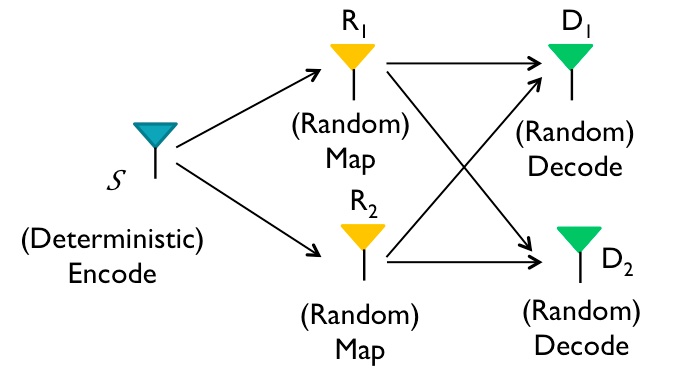 |
Relaying is a key feature proposed in the next generation of cellular networks in order to increase range (last mile coverage), increase capacity and to decrease network outage. When adding dedicated relays may prove to be expensive, existing users in the network can help relay information to other users (called user cooperation). While recent work has provided an approximate characterization of the information theoeretic capacity of relay networks, where a single source communicates to its destination through a network of relays, the characterization of capacity of broadcast networks remains open. In this project, we find the approximate capacity of downlink cellular networks with user cooperation and relaying. While it is hard to analyze the capacity of this networks directly, we create an operational connection to a determinisitic network, for which it is simpler to design provably near-optimal techniques. The proposed scheme has an interesting interpretation: the relays do random coding, and the destination fixes a decoding map, and then the source constructs a special codebook based on the realization of the codebooks used at the relays. S. Kannan, A. Raja, and P. Viswanath, Approximately Optimal Wireless Broadcasting, IEEE Trans. Info Theory, Dec. 2012. |
Interactive Interference Alignment
 |
Interference is a key bottleneck in modern wireless networks, and studying schemes that can manage interference well is an important topic of research. In this context, interference alignment has emerged as an important scheme with several attractive properties, however, the scheme is currently far from being practical. In this project, we study interference channels with the added feature of interaction, i.e., the destinations can talk back to the sources. The interaction can come in two ways: 1) for half-duplex radios, destinations can talk back to sources using either simultaneous out-of-band (white spaces) transmission or in-band half-duplex transmission; 2) for full-duplex radios, both sources and destinations can transmit and listen in the same channel simultaneously. The flexibility afforded by interaction among sources and destinations allows for the derivation of interference alignment (IA) strategies that have desirable “engineering properties”: insensitivity to the rationality or irrationality of channel parameters, small block lengths and finite SNR operations. We show that for "small" interference channels the interactive interference alignment scheme can achieve the optimal degrees of freedom. Q. Geng, S. Kannan, and P. Viswanath, Interactive Interference Alignment, IEEE JSAC, in submission. |
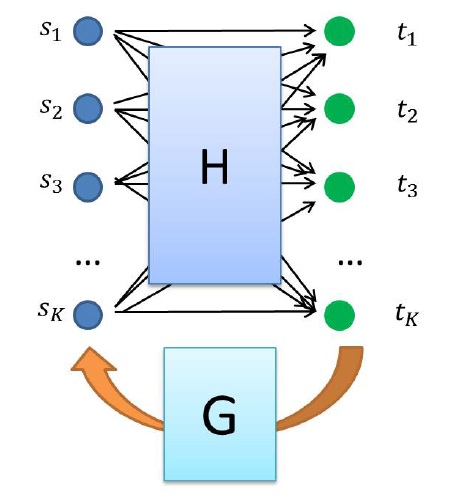
Distributed Function Computation
 |
In several scenarios, we are interested in computing some function of the data storied in different locations connected by a common communication infrastructure. This occurs, for example, in sensor networks where we want to compute a function of the sensor data or in cloud computing where data is stored on disks using a distributed storage system. In these contexts where communication is a key bottleneck, we are interested in the question of the capacity of function computation. In this project, we show that for many classes of functions, including symmetric functions, a simple scheme involving computation trees is near optimal if all the edges in the graph have bidirectional communication infrastructure. S. Kannan and P. Viswanath, Multi-session Function Computation in Undirected Graphs, JSAC, April 2013. |
Distributed Computing with Noise: Tree Codes
 |
With increasing miniaturization and voltage scaling, the buses connecting multiple distributed computing cores become ever more noisy. In order for the cores to execute their computation objective reliably, some form of error correction coding is mandatory. Error correction becomes complicated by the fact that bits cannot be blocked up into large chunks without first learning the output from the other cores. Therefore, a certain form of causal coding called tree coding has been proposed in the literature to deal with this problem. While existence of good tree codes have been known, how to construct one efficiently has not been well understood. In this project, we propose a new polynomial time construction of tree codes that succeeds with inverse quasi-polynomial probability. Y. Kalai, S. Kannan, and M. Sudan, A Randomized Construction of Tree Codes, in preparation. |